Introduction to statistical learning theory

Introduction to statistical learning theory

Date
27 Feb 2019
➡ 6 Mar 2019 ⬅
13 Mar 2019
20 Mar 2019
21 Mar 2019
Always at 12.00-14.00, except on 6 March
6 March: 15.00 – 17.00
❗New Location ❗
FME, room 001, Campus Sud, UPC
Only on 21 Mar, room 005
(Map here)

Summary

The theory of Machine Learning is a field that lies at the intersection of statistics, probability, computer science, and optimization. This mathematical theory is concerned with theoretical guarantees for machine learning algorithms. Over the last decades the statistical learning approach has been successfully applied to many problems of interest in machine learning, such as bioinformatics, computer vision, speech processing, robotics, and information retrieval. This success story crucially relies on a strong mathematical foundation.

The goal of this 10-hour course is to lay out some of the basic principles and introduce mathematical tools that help understand and analyze machine learning algorithms.

The focus will be on elements of empirical processes, concentration inequalities, kernel methods, and stochastic optimization of convex functions.

The course will be mostly of interest to PhD students in probability, statistics, optimization, and theoretical computer science. Only some basic background in probability at graduate level is required.

Date
27 Feb 2019
➡ 6 Mar 2019 ⬅
13 Mar 2019
20 Mar 2019
21 Mar 2019
Always at 12.00-14.00, except on 6 March
6 March: 15.00 – 17.00
❗New Location ❗
FME, room 001, Campus Sud, UPC
Only on 21 Mar, room 005
(Map here)

Summary

The theory of Machine Learning is a field that lies at the intersection of statistics, probability, computer science, and optimization. This mathematical theory is concerned with theoretical guarantees for machine learning algorithms. Over the last decades the statistical learning approach has been successfully applied to many problems of interest in machine learning, such as bioinformatics, computer vision, speech processing, robotics, and information retrieval. This success story crucially relies on a strong mathematical foundation.

The goal of this 10-hour course is to lay out some of the basic principles and introduce mathematical tools that help understand and analyze machine learning algorithms.

The focus will be on elements of empirical processes, concentration inequalities, kernel methods, and stochastic optimization of convex functions.

The course will be mostly of interest to PhD students in probability, statistics, optimization, and theoretical computer science. Only some basic background in probability at graduate level is required.

[et_pb_event_inscription event_id=”34″ use_dropshadow=”off” _builder_version=”3.0.105″ header_font_size_tablet=”51″ header_line_height_tablet=”2″ meta_font_size_tablet=”51″ meta_line_height_tablet=”2″ body_font_size_tablet=”51″ body_line_height_tablet=”2″ _i=”1″ _address=”1.1.2.1″ /]
With the support of
Gábor Lugosi, ICREA  Research  Professor, BGSMath – Universitat  Pompeu Fabra

Biosketch

Gábor Lugosi graduated in electrical engineering at the Technical University of Budapest in 1987, and received his Ph.D. from the Hungarian Academy of Sciences in 1991. Since 1996, he has been at the Department of Economics, Pompeu Fabra University, Barcelona. In 2006 he became an ICREA research professor.

Research Interests

  • Theory of machine learning
  • Combinatorial statistics
  • Inequalities in probability
  • Random graphs and random structures
  • Information theory
Syllabus
Basic setup: Elements of decision theory; Risk minimization.

Concentration inequalities: Concentration of sums of independent random variables; Random projections; Mean estimation; Concentration of functions of independent random variables.

Empirical processes: Uniform convergence of relative frequencies; Vapnik-Chervonenkis theory (Rademacher averages, VC-dimension); Empirical risk minimization;

Large-margin classifiers.

Kernel methods: Generalized linear regression and classification; Reproducing kernel Hilbert spaces; The kernel trick.

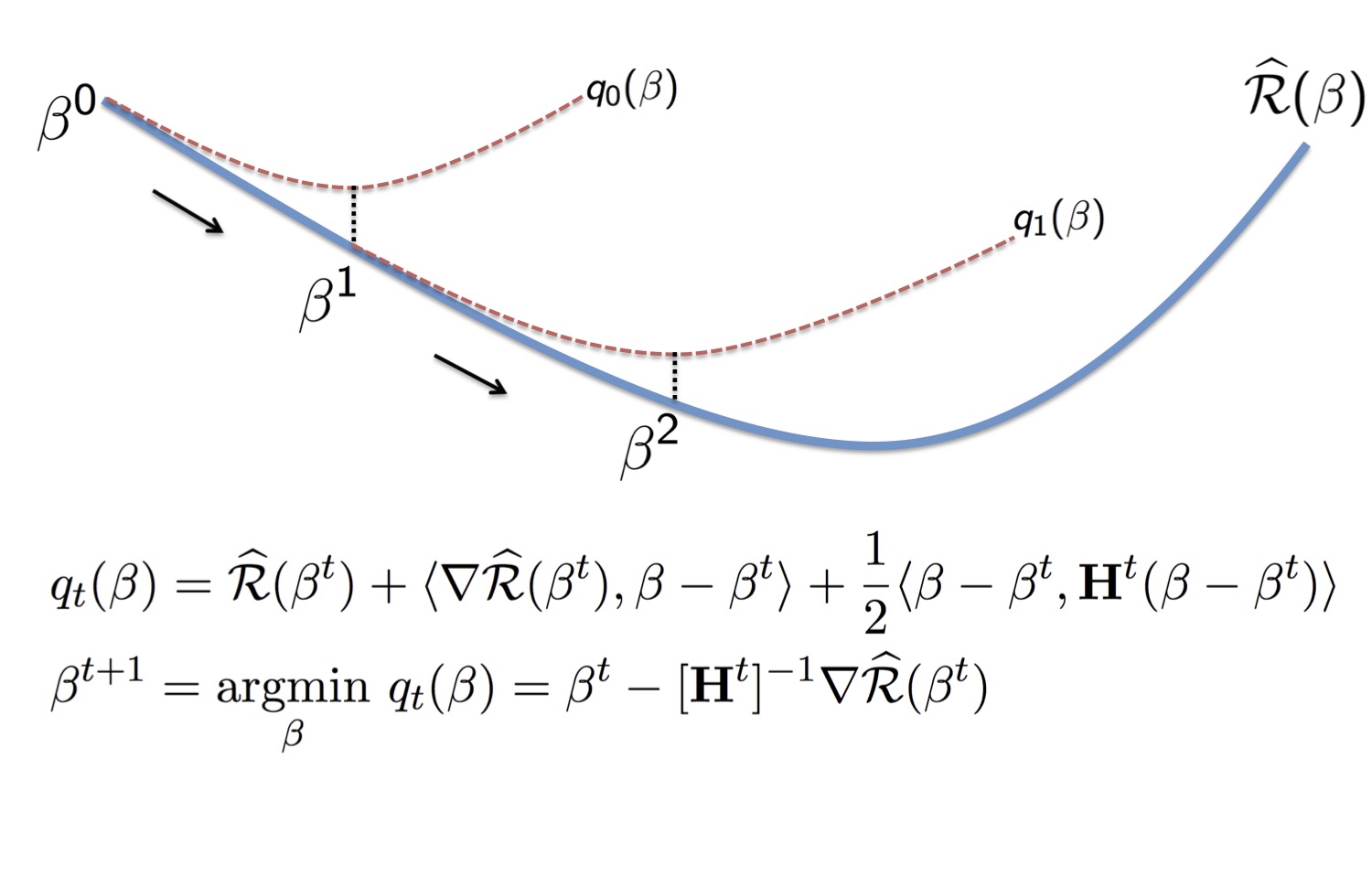
Elements of convex optimization: Stochastic optimization in machine learning; Stochastic gradient descent.

Bibliography
Shai Shalev-Shwartz and Shai Ben-David. Understanding Machine Learning. From Theory to Algorithms. Cambridge University Press, 2014.

Luc Devroye, László Györfi, Gábor Lugosi. A Probabilistic Theory of Pattern Recognition. Springer, 1996.

John Shawe-Taylor and Nello Crisianini. Kernel Methods for Pattern Analysis. Cambridge University Press, 2004.

Mehryar Mohri, Afshin Rostamizadeh, and Ameet Talwalkar. Foundations of Machine Learning. The MIT Press.

Martin Anthony and Peter L. Bartlett. Neural Network Learning: Theoretical Foundations. Cambridge University Press, 1999.

Stephane Boucheron, Olivier Bousquet and Gabor Lugosi. THEORY OF CLASSIFICATION: A SURVEY OF SOME RECENT ADVANCES. ESAIM: PS. November 2005, Vol. 9, p. 323–375.

Olivier Bousquet, Stéphane Boucheron, and Gábor Lugosi. Introduction to Statistical Learning Theory.