A Theory of Spectral Clustering
A Theory of Spectral Clustering
Date
21 Nov 2018
h. 15.30
h. 15.30
Location
Aula Màster del Campus Nord,
UPC
UPC
Abstract
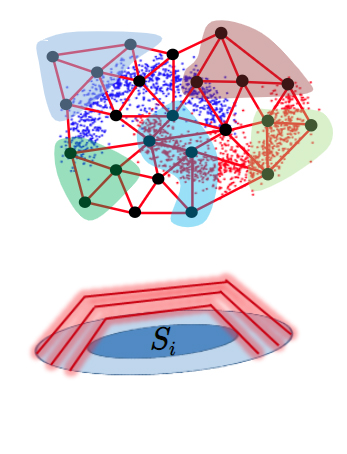
Spectral clustering algorithms find clusters in a given network by exploiting properties of the eigenvectors of matrices associated with the network. As a first step, one computes a spectral embedding, that is a mapping of nodes to points in a low-dimensional real space; then one uses geometric clustering algorithms such as k-means to cluster the points corresponding to the nodes.
Such algorithms work so well that, in certain applications unrelated to network analysis, such as image segmentation, it is useful to associate a network to the data, and then apply spectral clustering to the network. In addition to its application to clustering, spectral embeddings are a valuable tool for dimension-reduction and data visualization. The performance of spectral clustering algorithms has been justified rigorously when applied to networks coming from certain probabilistic generative models.
A more recent development, which is the focus of this lecture, is a worst-case analysis of spectral clustering, showing that, for every graph that exhibits a certain cluster structure, such structure can be found by geometric algorithms applied to a spectral embedding. Such results generalize the graph Cheeger’s inequality (a classical result in spectral graph theory), and they have additional applications in computational complexity theory and in pure mathematics.
Date
21 Nov 2018
h. 15.30
h. 15.30
Location
Aula Màster del Campus Nord,
UPC
UPC

Abstract
Spectral clustering algorithms find clusters in a given network by exploiting properties of the eigenvectors of matrices associated with the network. As a first step, one computes a spectral embedding, that is a mapping of nodes to points in a low-dimensional real space; then one uses geometric clustering algorithms such as k-means to cluster the points corresponding to the nodes.
Such algorithms work so well that, in certain applications unrelated to network analysis, such as image segmentation, it is useful to associate a network to the data, and then apply spectral clustering to the network. In addition to its application to clustering, spectral embeddings are a valuable tool for dimension-reduction and data visualization. The performance of spectral clustering algorithms has been justified rigorously when applied to networks coming from certain probabilistic generative models.
A more recent development, which is the focus of this lecture, is a worst-case analysis of spectral clustering, showing that, for every graph that exhibits a certain cluster structure, such structure can be found by geometric algorithms applied to a spectral embedding. Such results generalize the graph Cheeger’s inequality (a classical result in spectral graph theory), and they have additional applications in computational complexity theory and in pure mathematics.

Luca Trevisan, University of Berkeley (USA)
Biosketch
Luca Trevisan is a professor of electrical engineering and computer sciences at U.C. Berkeley and a senior scientist at the Simons Institute for the Theory of Computing. Luca studied at the Sapienza University of Rome, he was a post-doc at MIT and at DIMACS, and he was on the faculty of Columbia University, U.C. Berkeley, and Stanford, before returning to Berkeley in 2014. Luca’s research is in theoretical computer science, and it is focused on computational complexity and graph algorithms. Luca received the STOC’97 Danny Lewin (best student paper) award, the 2000 Oberwolfach Prize, and the 2000 Sloan Fellowship. He was an invited speaker at the 2006 International Congress of Mathematicians.

